H2020-MSCA-IF-2019, Example: magnetic DWs
This page details how to obtain the magnetic textures in the presence of a FE domain boundary. We relax the Landau-Lifshitz-Bloch equation in the presence of large damping (),
(1)
where is the effective field. The parameters , , and are the electron gyromagnetic factor, BFO magnetization saturation density, and vacuum permeability. The Kernels block computes the relevant contributions from ,
[Kernels]
#---------------------------------------#
# #
# Time dependence #
# #
#---------------------------------------#
[./mag1_x_time]
type = TimeDerivative
variable = mag1_x
[../]
[./mag1_y_time]
type = TimeDerivative
variable = mag1_y
[../]
[./mag1_z_time]
type = TimeDerivative
variable = mag1_z
[../]
[./mag2_x_time]
type = TimeDerivative
variable = mag2_x
[../]
[./mag2_y_time]
type = TimeDerivative
variable = mag2_y
[../]
[./mag2_z_time]
type = TimeDerivative
variable = mag2_z
[../]
#---------------------------------------#
# #
# AFM sublattice exchange #
# #
#---------------------------------------#
[./afmex1_x]
type = AFMSublatticeSuperexchange
variable = mag1_x
mag_sub = 0
component = 0
[../]
[./afmex1_y]
type = AFMSublatticeSuperexchange
variable = mag1_y
mag_sub = 0
component = 1
[../]
[./afmex1_z]
type = AFMSublatticeSuperexchange
variable = mag1_z
mag_sub = 0
component = 2
[../]
[./afmex2_x]
type = AFMSublatticeSuperexchange
variable = mag2_x
mag_sub = 1
component = 0
[../]
[./afmex2_y]
type = AFMSublatticeSuperexchange
variable = mag2_y
mag_sub = 1
component = 1
[../]
[./afmex2_z]
type = AFMSublatticeSuperexchange
variable = mag2_z
mag_sub = 1
component = 2
[../]
#---------------------------------------#
# #
# AFM sublattice DMI #
# #
#---------------------------------------#
[./afmdmi1_x]
type = AFMSublatticeDMInteraction
variable = mag1_x
mag_sub = 0
component = 0
[../]
[./afmdmi1_y]
type = AFMSublatticeDMInteraction
variable = mag1_y
mag_sub = 0
component = 1
[../]
[./afmdmi1_z]
type = AFMSublatticeDMInteraction
variable = mag1_z
mag_sub = 0
component = 2
[../]
[./afmdmi2_x]
type = AFMSublatticeDMInteraction
variable = mag2_x
mag_sub = 1
component = 0
[../]
[./afmdmi2_y]
type = AFMSublatticeDMInteraction
variable = mag2_y
mag_sub = 1
component = 1
[../]
[./afmdmi2_z]
type = AFMSublatticeDMInteraction
variable = mag2_z
mag_sub = 1
component = 2
[../]
#---------------------------------------#
# #
# Magnetocrystalline anisotropy for #
# the AFM sublattice in easy-plane #
# #
#---------------------------------------#
[./afma1_x]
type = AFMEasyPlaneAnisotropy
variable = mag1_x
mag_sub = 0
component = 0
[../]
[./afma1_y]
type = AFMEasyPlaneAnisotropy
variable = mag1_y
mag_sub = 0
component = 1
[../]
[./afma1_z]
type = AFMEasyPlaneAnisotropy
variable = mag1_z
mag_sub = 0
component = 2
[../]
[./afma2_x]
type = AFMEasyPlaneAnisotropy
variable = mag2_x
mag_sub = 1
component = 0
[../]
[./afma2_y]
type = AFMEasyPlaneAnisotropy
variable = mag2_y
mag_sub = 1
component = 1
[../]
[./afma2_z]
type = AFMEasyPlaneAnisotropy
variable = mag2_z
mag_sub = 1
component = 2
[../]
#---------------------------------------#
# #
# Single-ion anisotropy environment #
# for the AFM sublattice in the #
# degenerate easy-plane #
# #
#---------------------------------------#
[./afmsia1_x]
type = AFMSingleIonCubicSixthAnisotropy
variable = mag1_x
mag_sub = 0
component = 0
[../]
[./afmsia1_y]
type = AFMSingleIonCubicSixthAnisotropy
variable = mag1_y
mag_sub = 0
component = 1
[../]
[./afmsia1_z]
type = AFMSingleIonCubicSixthAnisotropy
variable = mag1_z
mag_sub = 0
component = 2
[../]
[./afmsia2_x]
type = AFMSingleIonCubicSixthAnisotropy
variable = mag2_x
mag_sub = 1
component = 0
[../]
[./afmsia2_y]
type = AFMSingleIonCubicSixthAnisotropy
variable = mag2_y
mag_sub = 1
component = 1
[../]
[./afmsia2_z]
type = AFMSingleIonCubicSixthAnisotropy
variable = mag2_z
mag_sub = 1
component = 2
[../]
#---------------------------------------#
# #
# LLB constraint terms #
# #
#---------------------------------------#
[./llb1_x]
type = LongitudinalLLB
variable = mag1_x
mag_x = mag1_x
mag_y = mag1_y
mag_z = mag1_z
component = 0
[../]
[./llb1_y]
type = LongitudinalLLB
variable = mag1_y
mag_x = mag1_x
mag_y = mag1_y
mag_z = mag1_z
component = 1
[../]
[./llb1_z]
type = LongitudinalLLB
variable = mag1_z
mag_x = mag1_x
mag_y = mag1_y
mag_z = mag1_z
component = 2
[../]
[./llb2_x]
type = LongitudinalLLB
variable = mag2_x
mag_x = mag2_x
mag_y = mag2_y
mag_z = mag2_z
component = 0
[../]
[./llb2_y]
type = LongitudinalLLB
variable = mag2_y
mag_x = mag2_x
mag_y = mag2_y
mag_z = mag2_z
component = 1
[../]
[./llb2_z]
type = LongitudinalLLB
variable = mag2_z
mag_x = mag2_x
mag_y = mag2_y
mag_z = mag2_z
component = 2
[../]
#---------------------------------------#
# #
# Local magnetic exchange #
# #
#---------------------------------------#
[./dllg1_x_exch]
type = ExchangeCartLL
variable = mag1_x
component = 0
mag_x = mag1_x
mag_y = mag1_y
mag_z = mag1_z
[../]
[./dllg1_y_exch]
type = ExchangeCartLL
variable = mag1_y
component = 1
mag_x = mag1_x
mag_y = mag1_y
mag_z = mag1_z
[../]
[./dllg1_z_exch]
type = ExchangeCartLL
variable = mag1_z
component = 2
mag_x = mag1_x
mag_y = mag1_y
mag_z = mag1_z
[../]
[./dllg2_x_exch]
type = ExchangeCartLL
variable = mag2_x
component = 0
mag_x = mag2_x
mag_y = mag2_y
mag_z = mag2_z
[../]
[./dllg2_y_exch]
type = ExchangeCartLL
variable = mag2_y
component = 1
mag_x = mag2_x
mag_y = mag2_y
mag_z = mag2_z
[../]
[./dllg2_z_exch]
type = ExchangeCartLL
variable = mag2_z
component = 2
mag_x = mag2_x
mag_y = mag2_y
mag_z = mag2_z
[../]
#---------------------------------------#
# #=
# Local AFM magnetic exchange #
# (Local-term) #
#---------------------------------------#
[./dllg1afm_x_exch]
type = AFMLocalSublatticeExchangeCartLL
variable = mag1_x
mag_sub = 0
component = 0
[../]
[./dllg1afm_y_exch]
type = AFMLocalSublatticeExchangeCartLL
variable = mag1_y
mag_sub = 0
component = 1
[../]
[./dllg1afm_z_exch]
type = AFMLocalSublatticeExchangeCartLL
variable = mag1_z
mag_sub = 0
component = 2
[../]
[./dllg2afm_x_exch]
type = AFMLocalSublatticeExchangeCartLL
variable = mag2_x
mag_sub = 1
component = 0
[../]
[./dllg2afm_y_exch]
type = AFMLocalSublatticeExchangeCartLL
variable = mag2_y
mag_sub = 1
component = 1
[../]
[./dllg2afm_z_exch]
type = AFMLocalSublatticeExchangeCartLL
variable = mag2_z
mag_sub = 1
component = 2
[../]
[]
We refer the reader to the Syntax page for relevant information on the residual and jacobian contributions constructed in the Kernels. Note that is the total magnetic energy split between a component () that does not depend on the information of the structural order and a component that does (). Therefore, one needs to load in the and as an initial condition. For this, we use the previous example calculation but refined slightly (use BFO_dwP1A1_100_ref.e from the tutorials folder). We use refinement so that the magnetic solution to the LLG-LLB equation is numerically stable. We load BFO_dwP1A1_100_ref.e with the Mesh block,
[Mesh]
[fileload]
type = FileMeshGenerator
file = BFO_dwP1A1_100_ref.e
use_for_exodus_restart = true
[]
[]
Next, we define the variables to solve for in the problem () in the Variables block,
[Variables]
[./mag1_x]
order = FIRST
family = LAGRANGE
[./InitialCondition]
type = FunctionIC
function = stripem1x
[../]
[../]
[./mag1_y]
order = FIRST
family = LAGRANGE
[./InitialCondition]
type = FunctionIC
function = stripem1y
[../]
[../]
[./mag1_z]
order = FIRST
family = LAGRANGE
[./InitialCondition]
type = FunctionIC
function = stripem1z
[../]
[../]
[./mag2_x]
order = FIRST
family = LAGRANGE
[./InitialCondition]
type = FunctionIC
function = stripem2x
[../]
[../]
[./mag2_y]
order = FIRST
family = LAGRANGE
[./InitialCondition]
type = FunctionIC
function = stripem2y
[../]
[../]
[./mag2_z]
order = FIRST
family = LAGRANGE
[./InitialCondition]
type = FunctionIC
function = stripem2z
[../]
[../]
[]
Note that and are postprocessed as AuxVariables.
We select an initial condition with the FunctionIC and ParsedFunction classes that corresponds to a possible rotation of (using functions). However, this is not stable and the system evolves to minimize gradients in . Different walls can be simulated by changing the initial conditions of or by swapping out for different orientations. The boundary conditions of this problem are very simple,
[BCs]
#---------------------------------------#
# #
# periodic magnetization distribution #
# #
#---------------------------------------#
[./Periodic]
[./x]
auto_direction = 'x'
variable = 'mag1_x mag1_y mag1_z mag2_x mag2_y mag2_z'
[../]
[../]
[]
with being the long direction of the computational volume. Relaxation of with this mesh takes around 5260 seconds on 6 processors using the WSL distribution of MOOSE. We supply the reader with the output of this mesh file if needed. The Executioner options,
[Executioner]
type = Transient
solve_type = 'NEWTON'
[./TimeIntegrator]
type = NewmarkBeta
[../]
dtmin = 1e-18
dtmax = 1e-7
[./TimeStepper]
type = IterationAdaptiveDT
optimal_iterations = 25 #usually 10
linear_iteration_ratio = 100
dt = 1e-9
growth_factor = 1.1
[../]
num_steps = 18001
[]
sets the time integration method as NewmarkBeta with an upper limit of ps. The DW profile of can be visualized in ParaView by using the PlotOverLine filter and could like the below figure,
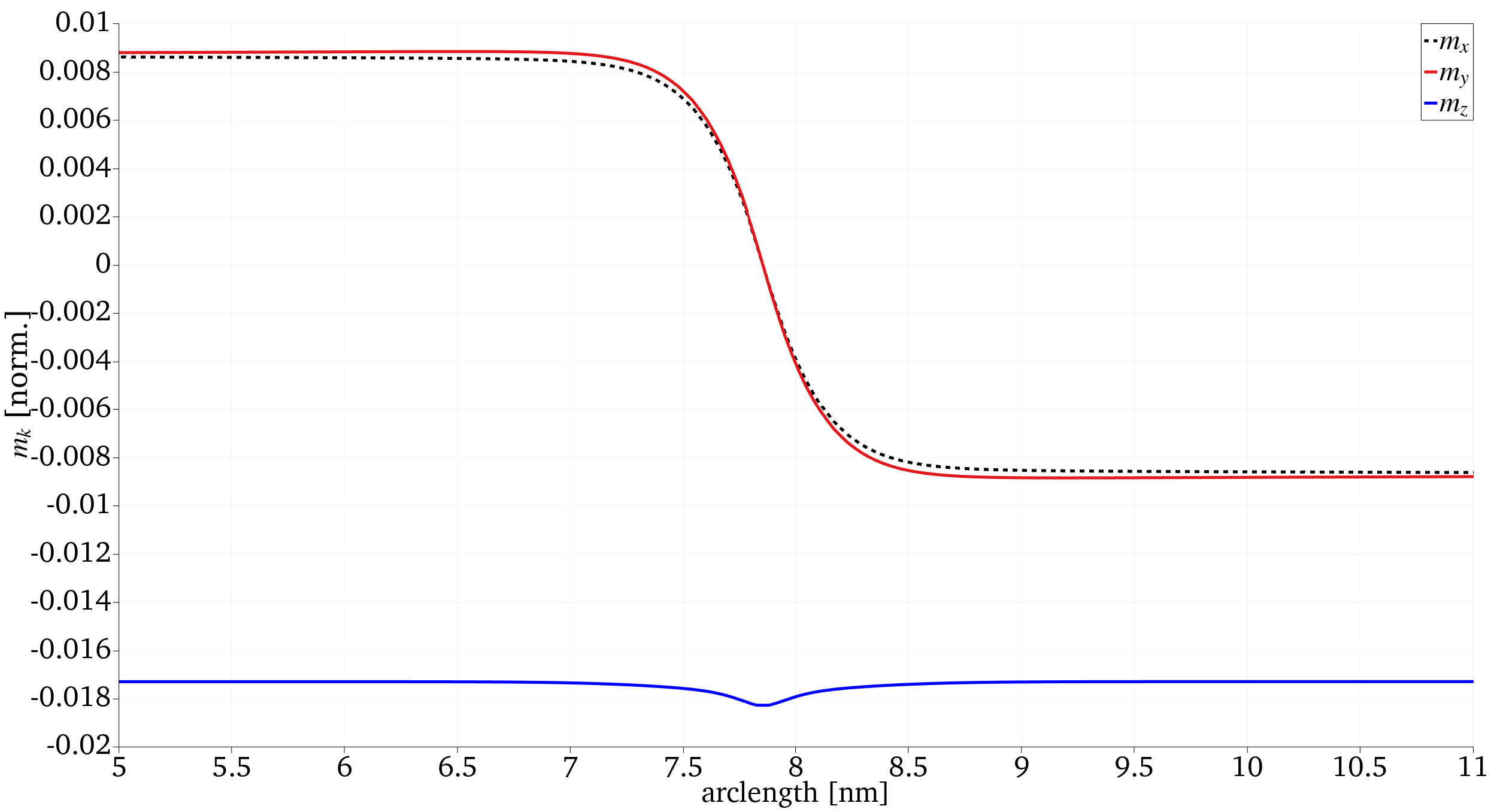
Figure 1: Components of across the 1/1 (100) DW. The net magnetization switches by .
-------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
This project SCALES - 897614 was funded for 2021-2023 at the Luxembourg Institute of Science and Technology under principle investigator Jorge Íñiguez-González. The research was carried out within the framework of the Marie Skłodowska-Curie Action (H2020-MSCA-IF-2019) fellowship.

-------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------