List of tutorials
All tutorials are written assuming that you are reasonably familiar with MOOSE. If you find most of the tutorials difficult to follow, please refer to the official MOOSE website for learning resources.
Tutorial 4: Ferromagnetic ringdown
This tutorial (and others) covers the basic usage of the micromagnetics implemented in FERRET. This simple problem is for solving the time-dependent LLG equation with exchange stiffness and demagnetizing field phenomena in a permalloy magnet. The total energy density of the system is written as
where and . The coefficient is the exchange stiffness parameter, the saturation magnetization density, and the magnetostatic potential.
We consider a magnetic body with a geometry which we define with the Mesh block.
[Mesh]
[./mesh]
type = GeneratedMeshGenerator
dim = 3
nx = 50
ny = 50
nz = 10
xmin = -50
xmax = 50
ymin = -50
ymax = 50
zmin = -10
zmax = 10
[../]
[./vacuum_box]
type = SubdomainBoundingBoxGenerator
input = mesh
bottom_left = '-50 -50 -10'
top_right = '50 50 10'
block_id = 2
block_name = vacuum
[../]
[./brick]
type = SubdomainBoundingBoxGenerator
input = vacuum_box
bottom_left = '-10 -10 -1.5'
top_right = '10 10 1.5'
block_id = 1
block_name = brick
[../]
[../]
In general, the geometry defined in the 'Mesh' block never carries units. The length scale is introduced through Materials, Kernels, or other MOOSE objects. More on this later in this tutorial. Note that the total computational domain is . The remaining area is defined as a vacuum block which acts as a numerical resource in order to solve for the demagnetizing field far from the magnetic body. In principle, we should take the limit which is impossible in a numerical simulation so the volume that is used must be large enough such that the field from the magnetic body naturally goes to zero. We suggest that if the vacuum block approach is used, one should likely test a number of distances to ensure the expected dependence of the demagnetizing field. We use the MOOSE object SubdomainBoundingBoxGenerator to split the mesh into two blocks. In this problem,
[Variables]
[./mag_x]
order = FIRST
family = LAGRANGE
block = '1'
[./InitialCondition]
type = RandomConstrainedVectorFieldIC
phi = azimuth_phi
theta = polar_theta
M0s = 1.0 #amplitude of the RandomConstrainedVectorFieldIC
component = 0
[../]
[../]
[./mag_y]
order = FIRST
family = LAGRANGE
block = '1'
[./InitialCondition]
type = RandomConstrainedVectorFieldIC
phi = azimuth_phi
theta = polar_theta
M0s = 1.0
component = 1
[../]
[../]
[./mag_z]
order = FIRST
family = LAGRANGE
block = '1'
[./InitialCondition]
type = RandomConstrainedVectorFieldIC
phi = azimuth_phi
theta = polar_theta
M0s = 1.0
component = 2
[../]
[../]
[./potential_H_int]
order = FIRST
family = LAGRANGE
block = '1 2'
[../]
[]
shows that we are only solving for the variables , and . The initial conditions (ICs) are seeded via spherical coordinates using RandomConstrainedVectorFieldIC to ensure that the ICs satisfy the normalization condition of the LLG equation, .
The micromagnetic problem solves the LLG-LLB equation,
(1)
with . The LLG-LLB equation is partitioned into a few Kernel objects for computation. We separate contributions component-wise and also by specific effective fields (in this case exchange stiffness and demagnetizing fields). These Kernels are listed
[Kernels]
#---------------------------------------#
# #
# Time dependence #
# #
#---------------------------------------#
[./mag_x_time]
type = TimeDerivative
variable = mag_x
block = '1'
[../]
[./mag_y_time]
type = TimeDerivative
variable = mag_y
block = '1'
[../]
[./mag_z_time]
type = TimeDerivative
variable = mag_z
block = '1'
[../]
#---------------------------------------#
# #
# Local magnetic exchange #
# #
#---------------------------------------#
[./dllg_x_exch]
type = MasterExchangeCartLLG
variable = mag_x
component = 0
mag_x = mag_x
mag_y = mag_y
mag_z = mag_z
block = '1'
[../]
[./dllg_y_exch]
type = MasterExchangeCartLLG
variable = mag_y
component = 1
mag_x = mag_x
mag_y = mag_y
mag_z = mag_z
block = '1'
[../]
[./dllg_z_exch]
type = MasterExchangeCartLLG
variable = mag_z
component = 2
mag_x = mag_x
mag_y = mag_y
mag_z = mag_z
block = '1'
[../]
#---------------------------------------#
# #
# demagnetization field #
# #
#---------------------------------------#
[./d_HM_x]
type = MasterInteractionCartLLG
variable = mag_x
component = 0
block = '1'
[../]
[./d_HM_y]
type = MasterInteractionCartLLG
variable = mag_y
component = 1
block = '1'
[../]
[./d_HM_z]
type = MasterInteractionCartLLG
variable = mag_z
component = 2
block = '1'
[../]
#---------------------------------------#
# #
# LLB constraint terms #
# #
#---------------------------------------#
[./llb1_x]
type = MasterLongitudinalLLB
variable = mag_x
component = 0
block = '1'
[../]
[./llb1_y]
type = MasterLongitudinalLLB
variable = mag_y
component = 1
block = '1'
[../]
[./llb1_z]
type = MasterLongitudinalLLB
variable = mag_z
component = 2
block = '1'
[../]
#---------------------------------------#
# #
# Magnetostatic Poisson equation #
# #
#---------------------------------------#
[./int_pot_lap]
type = Electrostatics
variable = potential_H_int
block = '1 2'
[../]
[./int_bc_pot_lap]
type = MagHStrongCart
variable = potential_H_int
block = '1'
[../]
[]
where MasterExchangeCartLLG handles the terms involving the exchange stiffness energy density, MasterInteractionCartLLG involves the interaction with the demagnetizing or applied magnetic fields, MasterLongitudinalLLB is the longitudinal restoring term from the LLB approximation. Finally, we have MagHStrongCart and Electrostatics (the Laplace equation LHS ) for the magnetostatic Poisson equation solved at every time step. The user can click these hyperlinks to see the weak-form algebra necessary to construct the Kernel objects. The Materials block,
[Materials]
############################################################################
##
## material constants used.
##
############################################################################
[./constants]
type = GenericConstantMaterial
prop_names = ' alpha permittivity Ae Ms'
prop_values = '${alphadef} 1.0 1.3e-05 1.2'
block = '1'
[../]
[./a_long]
type = GenericFunctionMaterial
prop_names = 'alpha_long'
prop_values = 'bc_func_1'
block = '1'
[../]
[./constantsv]
type = GenericConstantMaterial
prop_names = ' alpha permittivity Ae Ms'
prop_values = '1 1.0 1.3e-05 .0'
block = '2'
[../]
[./a_longv]
type = GenericFunctionMaterial
prop_names = 'alpha_long'
prop_values = 'bc_func_1'
block = '2'
[../]
[]
shows the coefficients we will use. Note that is provided to change the time scale of the problem into nanoseconds. A possible visualization output of this tutorial problem using ParaView is provided below
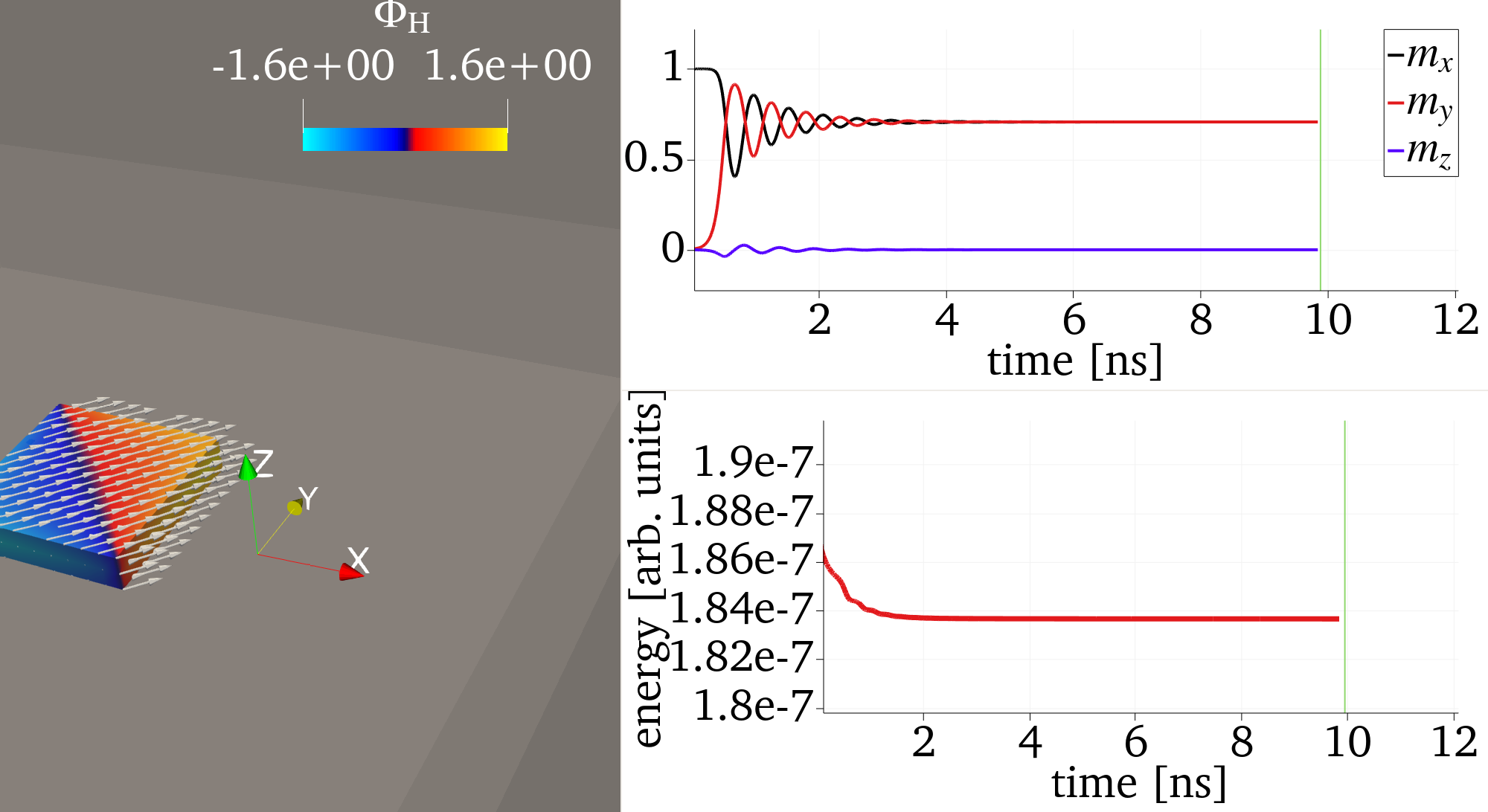
Figure 1: Left: Magnetic (normalized) texture in glyphs and the color map showing the contrast of the demagnetizing potential at the conclusion of the ringdown. The vacuum block is shown as slightly transparent. Top Right: components as a function of time during the ringdown. Bottom Right: Total energy as a function of time.