H2020-MSCA-IF-2019, Example: ME switching
This page details how to obtain ME switching trajectories in FERRET. We use an electric field to switch explicitly in a fully-time dependent simulation. The magnetization follows since any change in (and ) corresponds to a drastic change in the magnetic energy, , that couples to the structural distortions.
Our full approach involves solving the couple dynamic equation system,
(1)
for the structural order () along with,
at every time step, where and are the electro- and rotostrictive coefficients that couple and to the elastic strain respectively. For the spins, we solve,
(2)
Here, are a relaxation coefficients related to the time scales involved in the structural phase transition. The parameter is the electron gyromagnetic ratio and is the effective field acting on sublattice . The coeffiicent is a phenomenological damping constant which if made nonzero (and positive) drives the magnetic system to the ground state. We select a time-dependent electric field of the form,
(3)
which facilitates a reversal of the component. This means we expect the transition of to go from to orientation. For this problem, we use the input file BFO_P111_TO_P111b_switch_m1_a1.i located in the tutorials subdirectory. The Exodus input that we use corresponds to that of the second simulation in Example 1 (a fully relaxed polar-magnetic solution). We load this output as an input via the Mesh block,
[Mesh]
[fileload]
type = FileMeshGenerator
file = out_BFOMDL_P111A111_m1.e
use_for_exodus_restart = true
[]
[]
with corresponding flags in the Variables block,
[Variables]
[./mag1_x]
order = FIRST
family = LAGRANGE
initial_from_file_var = mag1_x
initial_from_file_timestep = 'LATEST'
[../]
[./mag1_y]
order = FIRST
family = LAGRANGE
initial_from_file_var = mag1_y
initial_from_file_timestep = 'LATEST'
[../]
[./mag1_z]
order = FIRST
family = LAGRANGE
initial_from_file_var = mag1_z
initial_from_file_timestep = 'LATEST'
[../]
[./mag2_x]
order = FIRST
family = LAGRANGE
initial_from_file_var = mag2_x
initial_from_file_timestep = 'LATEST'
[../]
[./mag2_y]
order = FIRST
family = LAGRANGE
initial_from_file_var = mag2_y
initial_from_file_timestep = 'LATEST'
[../]
[./mag2_z]
order = FIRST
family = LAGRANGE
initial_from_file_var = mag2_z
initial_from_file_timestep = 'LATEST'
[../]
[./u_x]
[../]
[./u_y]
[../]
[./u_z]
[../]
[./global_strain]
order = SIXTH
family = SCALAR
[../]
[./polar_x]
order = FIRST
family = LAGRANGE
initial_from_file_var = polar_x
initial_from_file_timestep = 'LATEST'
[../]
[./polar_y]
order = FIRST
family = LAGRANGE
initial_from_file_var = polar_y
initial_from_file_timestep = 'LATEST'
[../]
[./polar_z]
order = FIRST
family = LAGRANGE
initial_from_file_var = polar_z
initial_from_file_timestep = 'LATEST'
[../]
[./antiphase_A_x]
order = FIRST
family = LAGRANGE
initial_from_file_var = antiphase_A_x
initial_from_file_timestep = 'LATEST'
[../]
[./antiphase_A_y]
order = FIRST
family = LAGRANGE
initial_from_file_var = antiphase_A_y
initial_from_file_timestep = 'LATEST'
[../]
[./antiphase_A_z]
order = FIRST
family = LAGRANGE
initial_from_file_var = antiphase_A_z
initial_from_file_timestep = 'LATEST'
[../]
[]
The Kernels are due to structural evolution (TDLGD) along with the ones from micromagnetic evolution (LLG-LLB). They are listed in the following lengthy block,
[Kernels]
[./TensorMechanics]
[../]
[./rotostr_ux]
type = RotostrictiveCouplingDispDerivative
variable = u_x
component = 0
[../]
[./rotostr_uy]
type = RotostrictiveCouplingDispDerivative
variable = u_y
component = 1
[../]
[./rotostr_uz]
type = RotostrictiveCouplingDispDerivative
variable = u_z
component = 2
[../]
[./electrostr_ux]
type = ElectrostrictiveCouplingDispDerivative
variable = u_x
component = 0
[../]
[./electrostr_uy]
type = ElectrostrictiveCouplingDispDerivative
variable = u_y
component = 1
[../]
[./electrostr_uz]
type = ElectrostrictiveCouplingDispDerivative
variable = u_z
component = 2
[../]
### Operators for the polar field: ###
[./bed_x]
type = BulkEnergyDerivativeEighth
variable = polar_x
component = 0
[../]
[./bed_y]
type = BulkEnergyDerivativeEighth
variable = polar_y
component = 1
[../]
[./bed_z]
type = BulkEnergyDerivativeEighth
variable = polar_z
component = 2
[../]
[./roto_polar_coupled_x]
type = RotoPolarCoupledEnergyPolarDerivativeAlt
variable = polar_x
component = 0
[../]
[./roto_polar_coupled_y]
type = RotoPolarCoupledEnergyPolarDerivativeAlt
variable = polar_y
component = 1
[../]
[./roto_polar_coupled_z]
type = RotoPolarCoupledEnergyPolarDerivativeAlt
variable = polar_z
component = 2
[../]
[./roto_dis_coupled_x]
type = RotoPolarCoupledEnergyDistortDerivativeAlt
variable = antiphase_A_x
component = 0
[../]
[./roto_dis_coupled_y]
type = RotoPolarCoupledEnergyDistortDerivativeAlt
variable = antiphase_A_y
component = 1
[../]
[./roto_dis_coupled_z]
type = RotoPolarCoupledEnergyDistortDerivativeAlt
variable = antiphase_A_z
component = 2
[../]
[./electrostr_polar_coupled_x]
type = ElectrostrictiveCouplingPolarDerivative
variable = polar_x
component = 0
u_x = disp_x
u_y = disp_y
u_z = disp_z
[../]
[./electrostr_polar_coupled_y]
type = ElectrostrictiveCouplingPolarDerivative
variable = polar_y
component = 1
u_x = disp_x
u_y = disp_y
u_z = disp_z
[../]
[./electrostr_polar_coupled_z]
type = ElectrostrictiveCouplingPolarDerivative
variable = polar_z
component = 2
u_x = disp_x
u_y = disp_y
u_z = disp_z
[../]
#Operators for the AFD field
[./rbed_x]
type = RotoBulkEnergyDerivativeEighthAlt
variable = antiphase_A_x
component = 0
[../]
[./rbed_y]
type = RotoBulkEnergyDerivativeEighthAlt
variable = antiphase_A_y
component = 1
[../]
[./rbed_z]
type = RotoBulkEnergyDerivativeEighthAlt
variable = antiphase_A_z
component = 2
[../]
[./rotostr_dis_coupled_x]
type = RotostrictiveCouplingDistortDerivative
variable = antiphase_A_x
component = 0
u_x = disp_x
u_y = disp_y
u_z = disp_z
[../]
[./rotostr_dis_coupled_y]
type = RotostrictiveCouplingDistortDerivative
variable = antiphase_A_y
component = 1
u_x = disp_x
u_y = disp_y
u_z = disp_z
[../]
[./rotostr_dis_coupled_z]
type = RotostrictiveCouplingDistortDerivative
variable = antiphase_A_z
component = 2
u_x = disp_x
u_y = disp_y
u_z = disp_z
[../]
[./polar_electric_px]
type = PolarElectricPStrongEConst
variable = polar_x
component = 0
[../]
[./polar_electric_py]
type = PolarElectricPStrongEConst
variable = polar_y
component = 1
[../]
[./polar_electric_pz]
type = PolarElectricPStrongEConst
variable = polar_z
component = 2
[../]
#---------------------------------------#
# #
# Time dependence #
# #
#---------------------------------------#
[./mag1_x_time]
type = TimeDerivative
variable = mag1_x
[../]
[./mag1_y_time]
type = TimeDerivative
variable = mag1_y
[../]
[./mag1_z_time]
type = TimeDerivative
variable = mag1_z
[../]
[./mag2_x_time]
type = TimeDerivative
variable = mag2_x
[../]
[./mag2_y_time]
type = TimeDerivative
variable = mag2_y
[../]
[./mag2_z_time]
type = TimeDerivative
variable = mag2_z
[../]
#---------------------------------------#
# #
# AFM sublattice exchange #
# #
#---------------------------------------#
[./afmex1_x]
type = AFMSublatticeSuperexchange
variable = mag1_x
mag_sub = 0
component = 0
[../]
[./afmex1_y]
type = AFMSublatticeSuperexchange
variable = mag1_y
mag_sub = 0
component = 1
[../]
[./afmex1_z]
type = AFMSublatticeSuperexchange
variable = mag1_z
mag_sub = 0
component = 2
[../]
[./afmex2_x]
type = AFMSublatticeSuperexchange
variable = mag2_x
mag_sub = 1
component = 0
[../]
[./afmex2_y]
type = AFMSublatticeSuperexchange
variable = mag2_y
mag_sub = 1
component = 1
[../]
[./afmex2_z]
type = AFMSublatticeSuperexchange
variable = mag2_z
mag_sub = 1
component = 2
[../]
#---------------------------------------#
# #
# AFM sublattice DMI #
# !isStronglyCoupled=true #
#---------------------------------------#
[./afmdmi1_x]
type = AFMSublatticeDMInteractionSC
variable = mag1_x
mag_sub = 0
component = 0
[../]
[./afmdmi1_y]
type = AFMSublatticeDMInteractionSC
variable = mag1_y
mag_sub = 0
component = 1
[../]
[./afmdmi1_z]
type = AFMSublatticeDMInteractionSC
variable = mag1_z
mag_sub = 0
component = 2
[../]
[./afmdmi2_x]
type = AFMSublatticeDMInteractionSC
variable = mag2_x
mag_sub = 1
component = 0
[../]
[./afmdmi2_y]
type = AFMSublatticeDMInteractionSC
variable = mag2_y
mag_sub = 1
component = 1
[../]
[./afmdmi2_z]
type = AFMSublatticeDMInteractionSC
variable = mag2_z
mag_sub = 1
component = 2
[../]
#---------------------------------------#
# #
# Magnetocrystalline anisotropy for #
# the AFM sublattice in easy-plane #
# !isStronglyCoupled=true #
#---------------------------------------#
[./afma1_x]
type = AFMEasyPlaneAnisotropySC
variable = mag1_x
mag_sub = 0
component = 0
[../]
[./afma1_y]
type = AFMEasyPlaneAnisotropySC
variable = mag1_y
mag_sub = 0
component = 1
[../]
[./afma1_z]
type = AFMEasyPlaneAnisotropySC
variable = mag1_z
mag_sub = 0
component = 2
[../]
[./afma2_x]
type = AFMEasyPlaneAnisotropySC
variable = mag2_x
mag_sub = 1
component = 0
[../]
[./afma2_y]
type = AFMEasyPlaneAnisotropySC
variable = mag2_y
mag_sub = 1
component = 1
[../]
[./afma2_z]
type = AFMEasyPlaneAnisotropySC
variable = mag2_z
mag_sub = 1
component = 2
[../]
#---------------------------------------#
# #
# Single-ion anisotropy environment #
# for the AFM sublattice in the #
# degenerate easy-plane #
# !isStronglyCoupled=true #
#---------------------------------------#
[./afmsia1_x]
type = AFMSingleIonCubicSixthAnisotropySC
variable = mag1_x
mag_sub = 0
component = 0
[../]
[./afmsia1_y]
type = AFMSingleIonCubicSixthAnisotropySC
variable = mag1_y
mag_sub = 0
component = 1
[../]
[./afmsia1_z]
type = AFMSingleIonCubicSixthAnisotropySC
variable = mag1_z
mag_sub = 0
component = 2
[../]
[./afmsia2_x]
type = AFMSingleIonCubicSixthAnisotropySC
variable = mag2_x
mag_sub = 1
component = 0
[../]
[./afmsia2_y]
type = AFMSingleIonCubicSixthAnisotropySC
variable = mag2_y
mag_sub = 1
component = 1
[../]
[./afmsia2_z]
type = AFMSingleIonCubicSixthAnisotropySC
variable = mag2_z
mag_sub = 1
component = 2
[../]
#---------------------------------------#
# #
# LLB constraint terms #
# #
#---------------------------------------#
[./llb1_x]
type = LongitudinalLLB
variable = mag1_x
mag_x = mag1_x
mag_y = mag1_y
mag_z = mag1_z
component = 0
[../]
[./llb1_y]
type = LongitudinalLLB
variable = mag1_y
mag_x = mag1_x
mag_y = mag1_y
mag_z = mag1_z
component = 1
[../]
[./llb1_z]
type = LongitudinalLLB
variable = mag1_z
mag_x = mag1_x
mag_y = mag1_y
mag_z = mag1_z
component = 2
[../]
[./llb2_x]
type = LongitudinalLLB
variable = mag2_x
mag_x = mag2_x
mag_y = mag2_y
mag_z = mag2_z
component = 0
[../]
[./llb2_y]
type = LongitudinalLLB
variable = mag2_y
mag_x = mag2_x
mag_y = mag2_y
mag_z = mag2_z
component = 1
[../]
[./llb2_z]
type = LongitudinalLLB
variable = mag2_z
mag_x = mag2_x
mag_y = mag2_y
mag_z = mag2_z
component = 2
[../]
#---------------------------------------#
# #
# Time dependence #
# #
#---------------------------------------#
[./polar_x_time]
type = TimeDerivativeScaled
variable = polar_x
time_scale = 0.005
block = '0'
[../]
[./polar_y_time]
type = TimeDerivativeScaled
variable = polar_y
time_scale = 0.005
block = '0'
[../]
[./polar_z_time]
type = TimeDerivativeScaled
variable = polar_z
time_scale = 0.005
block = '0'
[../]
[./a_x_time]
type = TimeDerivativeScaled
variable = antiphase_A_x
time_scale = 0.00005
block = '0'
[../]
[./a_y_time]
type = TimeDerivativeScaled
variable = antiphase_A_y
time_scale = 0.00005
block = '0'
[../]
[./a_z_time]
type = TimeDerivativeScaled
variable = antiphase_A_z
time_scale = 0.00005
block = '0'
[../]
[]
For example, ElectrostrictiveCouplingDispDerivative and RotostrictiveCouplingDispDerivative correspond to the terms in the mechanical equilibrium condition involving and respectively,
The Kernel AFMEasyPlaneAnisotropySC corresponds to the RHS of,
(4)
where is the effective field due to the free energy density term responsible for easy-plane magnetic anisotropy,
(5)
which we compute as
(6)
The suffix SC in the name of this object corresponds to a strongly-coupled situation. This means that this object contributes non-zero jacobian contributions for . We refer the reader to our Syntax page for a extensive list of the Kernels in FERRET regarding this problem. We also evaluate a number of postprocessed quantities in the AuxKernels block,
[AuxKernels]
[./mag1_mag]
type = VectorMag
variable = mag1_s
vector_x = mag1_x
vector_y = mag1_y
vector_z = mag1_z
execute_on = 'initial timestep_end final'
[../]
[./mag2_mag]
type = VectorMag
variable = mag2_s
vector_x = mag2_x
vector_y = mag2_y
vector_z = mag2_z
execute_on = 'initial timestep_end final'
[../]
[./Neel_Lx]
type = VectorDiffOrSum
variable = Neel_L_x
var1 = mag1_x
var2 = mag2_x
diffOrSum = 0
execute_on = 'initial timestep_end final'
[../]
[./Neel_Ly]
type = VectorDiffOrSum
variable = Neel_L_y
var1 = mag1_y
var2 = mag2_y
diffOrSum = 0
execute_on = 'initial timestep_end final'
[../]
[./Neel_Lz]
type = VectorDiffOrSum
variable = Neel_L_z
var1 = mag1_z
var2 = mag2_z
diffOrSum = 0
execute_on = 'initial timestep_end final'
[../]
[./smallSignalMag_x]
type = VectorDiffOrSum
variable = SSMag_x
var1 = mag1_x
var2 = mag2_x
diffOrSum = 1
execute_on = 'initial timestep_end final'
[../]
[./smallSignalMag_y]
type = VectorDiffOrSum
variable = SSMag_y
var1 = mag1_y
var2 = mag2_y
diffOrSum = 1
execute_on = 'initial timestep_end final'
[../]
[./smallSignalMag_z]
type = VectorDiffOrSum
variable = SSMag_z
var1 = mag1_z
var2 = mag2_z
diffOrSum = 1
execute_on = 'initial timestep_end final'
[../]
[./phc]
type = AngleBetweenTwoVectors
variable = ph
var1x = mag1_x
var1y = mag1_y
var1z = mag1_z
var2x = mag2_x
var2y = mag2_y
var2z = mag2_z
execute_on = 'initial timestep_end final'
[../]
[./th1c]
type = AngleBetweenTwoVectors
variable = th1
var1x = mag1_x
var1y = mag1_y
var1z = mag1_z
var2x = polar_x
var2y = polar_y
var2z = polar_z
execute_on = 'initial timestep_end final'
[../]
[./th2c]
type = AngleBetweenTwoVectors
variable = th2
var1x = mag2_x
var1y = mag2_y
var1z = mag2_z
var2x = polar_x
var2y = polar_y
var2z = polar_z
execute_on = 'initial timestep_end final'
[../]
[./disp_x]
type = GlobalDisplacementAux
variable = disp_x
scalar_global_strain = global_strain
global_strain_uo = global_strain_uo
component = 0
[../]
[./disp_y]
type = GlobalDisplacementAux
variable = disp_y
scalar_global_strain = global_strain
global_strain_uo = global_strain_uo
component = 1
[../]
[./disp_z]
type = GlobalDisplacementAux
variable = disp_z
scalar_global_strain = global_strain
global_strain_uo = global_strain_uo
component = 2
[../]
[./s00]
type = RankTwoAux
variable = s00
rank_two_tensor = stress
index_i = 0
index_j = 0
[../]
[./s01]
type = RankTwoAux
variable = s01
rank_two_tensor = stress
index_i = 0
index_j = 1
[../]
[./s10]
type = RankTwoAux
variable = s10
rank_two_tensor = stress
index_i = 1
index_j = 0
[../]
[./s11]
type = RankTwoAux
variable = s11
rank_two_tensor = stress
index_i = 1
index_j = 1
[../]
[./e00]
type = RankTwoAux
variable = e00
rank_two_tensor = total_strain
index_i = 0
index_j = 0
[../]
[./e01]
type = RankTwoAux
variable = e01
rank_two_tensor = total_strain
index_i = 0
index_j = 1
[../]
[./e10]
type = RankTwoAux
variable = e10
rank_two_tensor = total_strain
index_i = 1
index_j = 0
[../]
[./e11]
type = RankTwoAux
variable = e11
rank_two_tensor = total_strain
index_i = 1
index_j = 1
[../]
[./e12]
type = RankTwoAux
variable = e12
rank_two_tensor = total_strain
index_i = 1
index_j = 2
[../]
[./e21]
type = RankTwoAux
variable = e21
rank_two_tensor = total_strain
index_i = 2
index_j = 1
[../]
[./e20]
type = RankTwoAux
variable = e20
rank_two_tensor = total_strain
index_i = 2
index_j = 0
[../]
[./e02]
type = RankTwoAux
variable = e02
rank_two_tensor = total_strain
index_i = 0
index_j = 2
[../]
[./e22]
type = RankTwoAux
variable = e22
rank_two_tensor = total_strain
index_i = 2
index_j = 2
[../]
[./ez]
type = HarmonicFieldAux
variable = E_z
amplitude = ${Eadef}
correction = 1.0
frequency = ${efreq}
tshift = 0.0
ton = 0.0
toff = 0.000944
execute_on = 'initial timestep_end final'
[../]
[./mcsublat1_phi]
type = SphericalCoordinateVector
variable = sublat1_phi
component = 0
var1x = mag1_x
var1y = mag1_y
var1z = mag1_z
execute_on = 'initial timestep_end final'
[../]
[./mcsublat1_th]
type = SphericalCoordinateVector
variable = sublat1_th
component = 1
var1x = mag1_x
var1y = mag1_y
var1z = mag1_z
execute_on = 'initial timestep_end final'
[../]
[./mcsublat2_phi]
type = SphericalCoordinateVector
variable = sublat2_phi
component = 0
var1x = mag2_x
var1y = mag2_y
var1z = mag2_z
execute_on = 'initial timestep_end final'
[../]
[./mcsublat2_th]
type = SphericalCoordinateVector
variable = sublat2_th
component = 1
var1x = mag2_x
var1y = mag2_y
var1z = mag2_z
execute_on = 'initial timestep_end final'
[../]
[]
For example, we compute and with VectorDiffOrSum. We also compute other values such as, i.e., the angular quantities and . Note that we use the convention that instead of unity. . The Materials block, assigns values to our coefficients,
[Materials]
[./constants]
# Constants used in other material properties
type = GenericConstantMaterial
prop_names = ' alpha De D0 g0mu0Ms g0 K1 K1c Kt '
prop_values = '0.003 3.7551 0.003 48291.9 48291.9 -5.0068 -0.00550748 -0.000365997 '
[../]
[./a_long]
type = GenericFunctionMaterial
prop_names = 'alpha_long'
prop_values = 'bc_func_1'
[../]
[./Landau_P]
type = GenericConstantMaterial
prop_names = 'alpha1 alpha11 alpha12 alpha111 alpha112 alpha123 alpha1111 alpha1112 alpha1122 alpha1123'
prop_values = '-2.81296e3 1.72351e3 2.24147e3 0.0 0.0 0.0 0.0 0.0 0.0 0.0'
[../]
[./Landau_A]
type = GenericConstantMaterial
prop_names = 'beta1 beta11 beta12 beta111 beta112 beta123 beta1111 beta1112 beta1122 beta1123'
prop_values = '-0.0137763e3 0.0000349266e3 0.0000498846e3 0.0 0.0 0.0 0.0 0.0 0.0 0.0'
[../]
[./P_A_couple]
type = GenericConstantMaterial
prop_names = 't1111 t1122 t1212 t42111111 t24111111 t42111122 t24112222 t42112233 t24112233 t42112211 t24111122 t42111212 t42123312 t24121112 t24121233 t6211111111 t2611111111 t6211111122 t2611222222 t4411111111 t4411112222'
prop_values = '0.012516e3 0.0180504e3 -0.036155e3 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0'
[../]
[./mat_C]
type = GenericConstantMaterial
prop_names = 'C11 C12 C44'
prop_values = '295.179e3 117.567e3 74.0701e3'
[../]
[./mat_Q]
type = GenericConstantMaterial
prop_names = 'Q11 Q12 Q44'
prop_values = '-0.0603833 0.0111245 -0.0175686'
[../]
[./mat_R]
type = GenericConstantMaterial
prop_names = 'R11 R12 R44'
prop_values = '-0.0000878064 0.0000295306 0.0000627962'
[../]
[./mat_q]
type = GenericConstantMaterial
prop_names = 'q11 q12 q44'
prop_values = '-30.4162e3 -5.01496e3 -10.4105e3'
#the point is the following: use a slightly different definition of Q_ij than Hlinka
[../]
[./mat_r]
type = GenericConstantMaterial
prop_names = 'r11 r12 r44'
prop_values = '-0.0379499e3 0.00373096e3 0.0372105e3'
[../]
[./elasticity_tensor_1]
type = ComputeElasticityTensor
fill_method = symmetric9
C_ijkl = '295.179e3 117.567e3 117.567e3 295.179e3 117.567e3 295.179e3 74.0701e3 74.0701e3 74.0701e3'
[../]
[./strain]
type = ComputeSmallStrain
global_strain = global_strain
[../]
[./global_strain]
type = ComputeGlobalStrain
scalar_global_strain = global_strain
global_strain_uo = global_strain_uo
[../]
[./stress]
type = ComputeLinearElasticStress
[../]
[./permitivitty_1]
###############################################
##
## so-called background dielectric constant
## (it encapsulates the motion of core electrons
## at high frequency) = e_b*e_0 (here we use
## e_b = 10), see PRB. 74, 104014, (2006)
##
###############################################
type = GenericConstantMaterial
prop_names = 'permittivity'
prop_values = '0.00008854187'
[../]
[]
where we have used units of nanometers, microseconds, attocoulombs, and picograms. This sets the time and length scales in this problem. The Executioner block, chooses flags for the time integration and numerical solve,
[Executioner]
type = Transient
solve_type = 'PJFNK'
[./TimeIntegrator]
type = ImplicitEuler
[../]
dtmin = 1e-14
dtmax = 1.0e-6
[./TimeStepper]
type = IterationAdaptiveDT
optimal_iterations = 18 #usually 8-16
linear_iteration_ratio = 100
dt = 1.0e-8
[../]
num_steps = 150000
end_time = ${endtdef}
[]
A possible visualization of the output using ParaView is provided below,
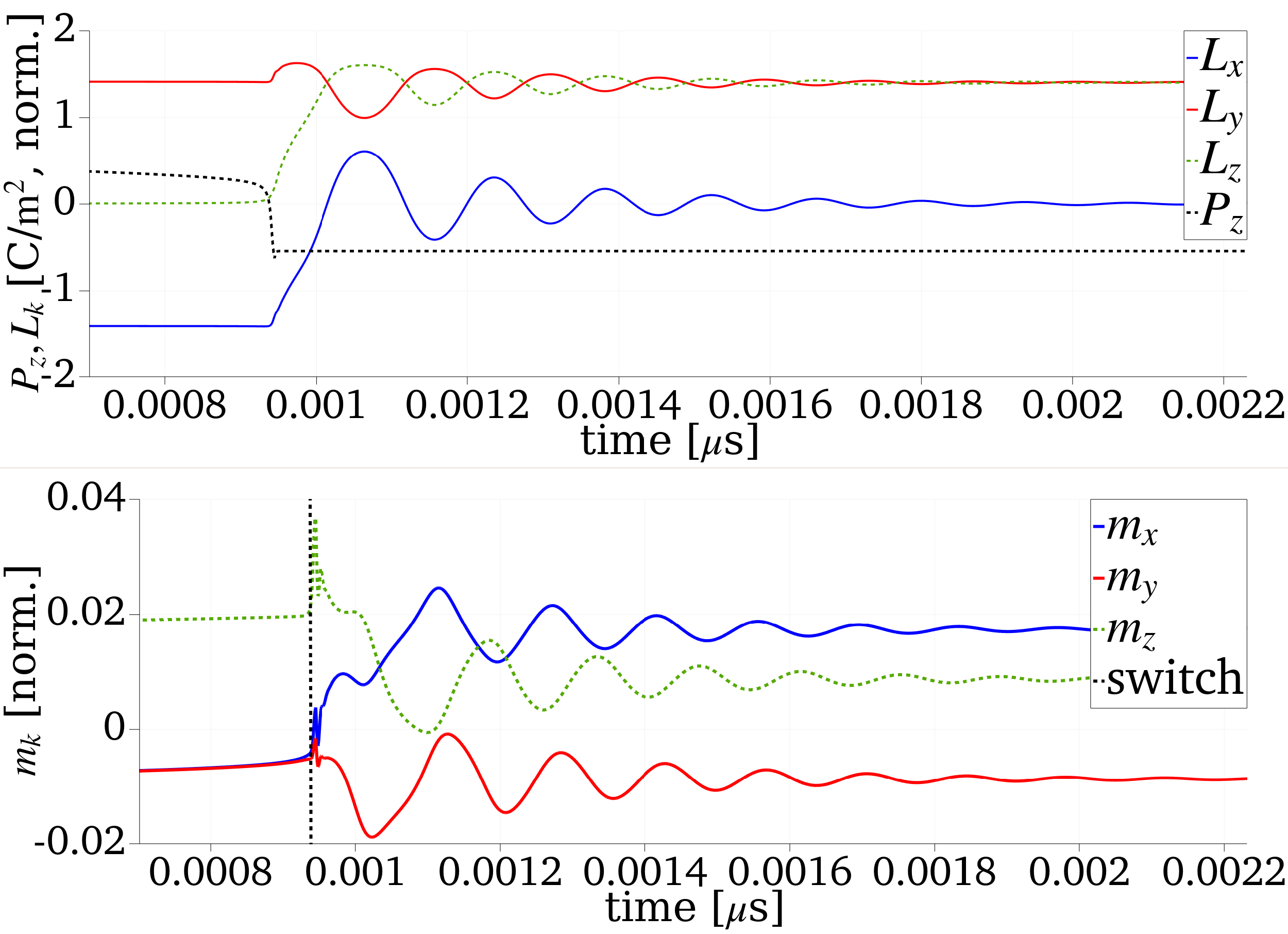
Figure 1: Homogeneous switching at with Top: Neel vector switching and Bottom: net magnetization switching. These dynamics are acquired using a time-dependent electric field at frequency MHz.
The wall clock time for this problem is 62.37 seconds on 6 processors using the WSL distribution of MOOSE. Note that other switching trajectories can be obtained by switching out the initial Exodus file - for example, choosing different six-fold orientation or by selecting a different orientation.
-------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
This project SCALES - 897614 was funded for 2021-2023 at the Luxembourg Institute of Science and Technology under principle investigator Jorge Íñiguez-González. The research was carried out within the framework of the Marie Skłodowska-Curie Action (H2020-MSCA-IF-2019) fellowship.

-------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------