- coefficientMaterial property name for the leading coefficient for Norton power law
C++ Type:MaterialPropertyName
Controllable:No
Description:Material property name for the leading coefficient for Norton power law
- powerStress exponent for Norton power law
C++ Type:double
Controllable:No
Description:Stress exponent for Norton power law
AD Viscoplasticity Stress Update
This material computes the non-linear homogenized gauge stress in order to compute the viscoplastic responce due to creep in porous materials. This material must be used in conjunction with ADComputeMultiplePorousInelasticStress
Description
ADViscoplasticityStressUpdate implements the Gurson-Tvergaard-Needleman (GTN) and Leblond-Perrin-Suqeut (LPS) following the theory described above. ADViscoplasticityStressUpdate uses similar techniques as ADRadialReturnStressUpdate to compute the gauge stress in order to correctly calculate the plastic strain in a porous material. ADViscoplasticityStressUpdate must be used in conjunction with ADComputeMultiplePorousInelasticStress in order to capture the porosity evolution.
Notation
Mean stress:
Microscopic stress:
Mean strain:
Microscopic strain:
Hydrostatic stress:
Deviatoric stress:
Equivalent stress:
Trace:
Porosity:
Stress exponent:
Theory
As pores nucleate within a material system, the dissipative potential that governs overall stress-strain response and drives local void growth mechanisms is enhanced. Simply put, the constitutive behavior of a material and the evolution of porosity within are highly coupled processes. In high-temperature and other extreme environments, this potential should include effects of viscoplasticity and diffusion.
Homogenization of a composite material's plastic potential can be accomplished using the Bishop and Hill (1951) upper-bound theorem for dissipation, which says that any possible dissipation field solved at the macroscopic level is an upper bound to the volume average of local dissipation within a material system.
In many continuum level modeling problems, the simulation length scale is larger than individual voids themselves, and therefore methods in homogenization are required to model the voided material response with an approximated, simplified medium. These methods aim to match the dissipative potential of the true medium Figure 1, thereby ensuring accurate stress-strain constitutive behavior of the porous material system.
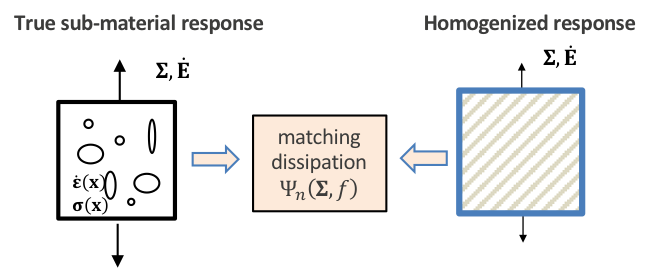
Figure 1: Schematic comparing the true sub-material response and the homogenized response and showing that the two methods match energy dissipation.
Gurson (1977) employed this approach to solve for dissipation in a purely-plastic (rate-insensitive) material, and derived an exact expression for the velocity and strain fields within a unit cell based on isotropic expressions of the Rice and Tracey (1969) fields. The solution to these velocity fields was derived using boundary conditions of strain at the surface of the unit cell, local incompressibility of the material system, and an overall minimization of work to bring the approximate upper-bound solution as close as possible to the true solution. In Gurson's formulation, it should be noted that despite incompressibility of the material itself, the overall unit cell (void + material) is in fact compressible due to the void. Therefore, void growth, can be modeled simply based on overall dilatation:
The exact result for average dissipation in the unit cell was correlated against an analytical solution so that it would be useful for application in finite element codes for large-scale component analysis. Several fitting parameters were introduced into Gurson's model by Tvergaard and Needleman (1984) to account for a periodic array of voids (rather than the original unit cell), leading to the famous GTN model that is the most widely-used damage and porosity evolution model for ductile materials.
Leblond et al. (1994) (LPS) extended the GTN model to account for rate-sensitive plastics. While far less common than the rate-insensitive GTN model, the work by Leblond et al. generated a similar analytical solution to GTN, but accounted for dissipation in the material, making it also very accessible to finite element implementation. It is expected that differences between rate-sensitive (i.e. LPS) and rate-insensitive (i.e. GTN) plasticity will become significant at lower temperatures and stresses. As such, the LPS model is selected for describing dissipation in a rate-sensitive voided material. In the case of a single dissipative potential, described by a Norton-type power law:
(1) (2) Here, the gauge stress, , is used to translate applied stress and porosity to strain rate response in a power law creeping material with rate-sensitivity factor , is given via the minimization of the residual : where is a rate sensitivity factor. The law proposed by Leblond et al. (1994)reduces exactly to the Gurson (1977) model when using a rate-insensitive exponent.
Implementation
The inelastic strain is currently calculated explicitly, where the strain rate is calculated via, (3) By taking the derivative of Eq. (3) with respect to the gauge stress, the familiar Norton power law is formed, (4) providing a clear link between traditional power law creep solves; by replacing utilized in tradiation power law creep equations with a gauge stress, the exact strain dissipation is captured due to the act of homogenization.
Using the LPS model, the gauge stress is calculated by minimizing the residual, (5)
The rate sensitivity factor is a function of the strain rate stress exponent, gauge stress, and equivalent stress, (6) where is a shape factor that depends on the pore shape: (7)
In addition, the mean stress utilized in Eq. (6) is different depending on the shape of the pore, (8)
The GTN can be solved in exactly the same manner as the LPS model by taking in Eq. (5) and Eq. (7), reducing to,
Once a solution for is found, the strain rate can be determined using Eq. (3) with the relationship,
Example Input Files
In all cases, ADViscoplasticityStressUpdate must be combined with ADComputeMultiplePorousInelasticStress in order to calculate the stress and capture the porosity evolution of the material:
[Materials]
[./elasticity_tensor]
type = ADComputeIsotropicElasticityTensor
youngs_modulus = 1e10
poissons_ratio = 0.3
[../]
[./stress]
type = ADComputeMultipleInelasticStress
inelastic_models = lps
outputs = all
[../]
[./porosity]
type = ADPorosityFromStrain
initial_porosity = 0.1
inelastic_strain = 'combined_inelastic_strain'
outputs = 'all'
[../]
[./lps]
type = ADViscoplasticityStressUpdate
coefficient = 'coef'
power = 3
outputs = all
relative_tolerance = 1e-11
[../]
[./coef]
type = ADParsedMaterial
property_name = coef
# Example of creep power law
expression = '1e-18 * exp(-4e4 / 1.987 / 1200)'
[../]
[]
In this case, the power law coefficient defined in Eq. (4) is provided as an example here as a ParsedMaterial. Note, if necessary, the coefficient must be provided as an AD material if variables or variable dependent materials are utilized to calculate coefficient.
If several different stress exponents are required, separate ADViscoplasticityStressUpdate must be specified, and combined in ADComputeMultiplePorousInelasticStress:
Here, materials calculated by ADViscoplasticityStressUpdate are prepended with base_name to separate their contributions to the overall system. Note, this is different than the base_name provided in the TensorMechanics Master Action
[Materials]
[./elasticity_tensor]
type = ADComputeIsotropicElasticityTensor
youngs_modulus = 1e10
poissons_ratio = 0.3
[../]
[./stress]
type = ADComputeMultipleInelasticStress
inelastic_models = 'one two'
outputs = all
[../]
[./porosity]
type = ADPorosityFromStrain
initial_porosity = 0.1
inelastic_strain = 'combined_inelastic_strain'
outputs = 'all'
[../]
[./one]
type = ADViscoplasticityStressUpdate
coefficient = 'coef_3'
power = 3
base_name = 'lps_1'
outputs = all
relative_tolerance = 1e-11
[../]
[./two]
type = ADViscoplasticityStressUpdate
coefficient = 1e-10
power = 1
base_name = 'lps_3'
outputs = all
relative_tolerance = 1e-11
[../]
[./coef]
type = ADParsedMaterial
property_name = coef_3
# Example of creep power law
coupled_variables = temp
expression = '0.5e-18 * exp(-4e4 / 1.987 / temp)'
[../]
[]
Input Parameters
- absolute_tolerance1e-11Absolute convergence tolerance for Newton iteration
Default:1e-11
C++ Type:double
Controllable:No
Description:Absolute convergence tolerance for Newton iteration
- acceptable_multiplier10Factor applied to relative and absolute tolerance for acceptable convergence if iterations are no longer making progress
Default:10
C++ Type:double
Controllable:No
Description:Factor applied to relative and absolute tolerance for acceptable convergence if iterations are no longer making progress
- automatic_differentiation_return_mappingFalseWhether to use automatic differentiation to compute the derivative.
Default:False
C++ Type:bool
Controllable:No
Description:Whether to use automatic differentiation to compute the derivative.
- base_nameOptional parameter that defines a prefix for all material properties related to this stress update model. This allows for multiple models of the same type to be used without naming conflicts.
C++ Type:std::string
Controllable:No
Description:Optional parameter that defines a prefix for all material properties related to this stress update model. This allows for multiple models of the same type to be used without naming conflicts.
- blockThe list of blocks (ids or names) that this object will be applied
C++ Type:std::vector<SubdomainName>
Controllable:No
Description:The list of blocks (ids or names) that this object will be applied
- boundaryThe list of boundaries (ids or names) from the mesh where this object applies
C++ Type:std::vector<BoundaryName>
Controllable:No
Description:The list of boundaries (ids or names) from the mesh where this object applies
- constant_onNONEWhen ELEMENT, MOOSE will only call computeQpProperties() for the 0th quadrature point, and then copy that value to the other qps.When SUBDOMAIN, MOOSE will only call computeQpProperties() for the 0th quadrature point, and then copy that value to the other qps. Evaluations on element qps will be skipped
Default:NONE
C++ Type:MooseEnum
Controllable:No
Description:When ELEMENT, MOOSE will only call computeQpProperties() for the 0th quadrature point, and then copy that value to the other qps.When SUBDOMAIN, MOOSE will only call computeQpProperties() for the 0th quadrature point, and then copy that value to the other qps. Evaluations on element qps will be skipped
- declare_suffixAn optional suffix parameter that can be appended to any declared properties. The suffix will be prepended with a '_' character.
C++ Type:MaterialPropertyName
Controllable:No
Description:An optional suffix parameter that can be appended to any declared properties. The suffix will be prepended with a '_' character.
- initial_porosity0Initial porosity
Default:0
C++ Type:double
Controllable:No
Description:Initial porosity
- max_inelastic_increment0.0001The maximum inelastic strain increment allowed in a time step
Default:0.0001
C++ Type:double
Controllable:No
Description:The maximum inelastic strain increment allowed in a time step
- minimum_equivalent_stress0.001Minimum value of equivalent stress below which viscoplasticiy is not calculated.
Default:0.001
C++ Type:double
Controllable:No
Description:Minimum value of equivalent stress below which viscoplasticiy is not calculated.
- negative_behaviorINITIAL_CONDITIONEnum how to handle negative porosities
Default:INITIAL_CONDITION
C++ Type:MooseEnum
Controllable:No
Description:Enum how to handle negative porosities
- pore_shape_modelsphericalWhich pore shape model to use
Default:spherical
C++ Type:MooseEnum
Controllable:No
Description:Which pore shape model to use
- porosity_nameporosityName of porosity material property
Default:porosity
C++ Type:MaterialPropertyName
Controllable:No
Description:Name of porosity material property
- prop_getter_suffixAn optional suffix parameter that can be appended to any attempt to retrieve/get material properties. The suffix will be prepended with a '_' character.
C++ Type:MaterialPropertyName
Controllable:No
Description:An optional suffix parameter that can be appended to any attempt to retrieve/get material properties. The suffix will be prepended with a '_' character.
- relative_tolerance1e-08Relative convergence tolerance for Newton iteration
Default:1e-08
C++ Type:double
Controllable:No
Description:Relative convergence tolerance for Newton iteration
- total_strain_base_nameBase name for the total strain
C++ Type:std::string
Controllable:No
Description:Base name for the total strain
- viscoplasticity_modelLPSWhich viscoplastic model to use
Default:LPS
C++ Type:MooseEnum
Controllable:No
Description:Which viscoplastic model to use
Optional Parameters
- control_tagsAdds user-defined labels for accessing object parameters via control logic.
C++ Type:std::vector<std::string>
Controllable:No
Description:Adds user-defined labels for accessing object parameters via control logic.
- enableTrueSet the enabled status of the MooseObject.
Default:True
C++ Type:bool
Controllable:Yes
Description:Set the enabled status of the MooseObject.
- implicitTrueDetermines whether this object is calculated using an implicit or explicit form
Default:True
C++ Type:bool
Controllable:No
Description:Determines whether this object is calculated using an implicit or explicit form
- inelastic_strain_nameviscoplasticityName of the material property that stores the effective inelastic strain
Default:viscoplasticity
C++ Type:std::string
Controllable:No
Description:Name of the material property that stores the effective inelastic strain
- maximum_equivalent_stress1e+12Maximum value of equivalent stress above which an exception is thrown instead of calculating the properties in this material.
Default:1e+12
C++ Type:double
Controllable:No
Description:Maximum value of equivalent stress above which an exception is thrown instead of calculating the properties in this material.
- maximum_gauge_ratio1e+06Maximum ratio between the gauge stress and the equivalent stress. This should be a high number. Note that this does not set an upper bound on the value, but rather will help with convergence of the inner Newton loop
Default:1e+06
C++ Type:double
Controllable:No
Description:Maximum ratio between the gauge stress and the equivalent stress. This should be a high number. Note that this does not set an upper bound on the value, but rather will help with convergence of the inner Newton loop
- seed0The seed for the master random number generator
Default:0
C++ Type:unsigned int
Controllable:No
Description:The seed for the master random number generator
- use_displaced_meshFalseWhether or not this object should use the displaced mesh for computation. Note that in the case this is true but no displacements are provided in the Mesh block the undisplaced mesh will still be used.
Default:False
C++ Type:bool
Controllable:No
Description:Whether or not this object should use the displaced mesh for computation. Note that in the case this is true but no displacements are provided in the Mesh block the undisplaced mesh will still be used.
- verboseFalseFlag to output verbose information
Default:False
C++ Type:bool
Controllable:No
Description:Flag to output verbose information
Advanced Parameters
- internal_solve_full_iteration_historyFalseSet true to output full internal Newton iteration history at times determined by `internal_solve_output_on`. If false, only a summary is output.
Default:False
C++ Type:bool
Controllable:No
Description:Set true to output full internal Newton iteration history at times determined by `internal_solve_output_on`. If false, only a summary is output.
- internal_solve_output_onon_errorWhen to output internal Newton solve information
Default:on_error
C++ Type:MooseEnum
Controllable:No
Description:When to output internal Newton solve information
Debug Parameters
- output_propertiesList of material properties, from this material, to output (outputs must also be defined to an output type)
C++ Type:std::vector<std::string>
Controllable:No
Description:List of material properties, from this material, to output (outputs must also be defined to an output type)
- outputsnone Vector of output names where you would like to restrict the output of variables(s) associated with this object
Default:none
C++ Type:std::vector<OutputName>
Controllable:No
Description:Vector of output names where you would like to restrict the output of variables(s) associated with this object
Outputs Parameters
References
- J F W Bishop and R Hill.
A theory of the plastic distortion of a polycrystalline aggregate under combined stresses.
The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 42(327):414–427, 1951.[BibTeX]
- A L Gurson.
Continuum Theory of Ductile Rupture by Void Nucleation and Growth: Part I—Yield Criteria and Flow Rules for Porous Ductile Media.
Journal of Engineering Materials and Technology, 99(1):2–63, 1977.[BibTeX]
- J B Leblond, G Perrin, and P Suquet.
Exact results and approximate models for porous viscoplastic solids.
International Journal of Plasticity, 10(3):213–235, January 1994.[BibTeX]
- J R Rice and D M Tracey.
On the ductile enlargement of voids in triaxial stress fields.
Journal of the Mechanics and Physics of Solids, 17(3):201–217, 1969.[BibTeX]
- V Tvergaard and A Needleman.
Analysis of the cup-cone fracture in a round tensile bar.
Acta Metallurgica, 32(1):157–169, 1984.[BibTeX]