Compute Multiple Crystal Plasticity Stress

Constitutive Equations

For finite strain inelastic mechanics of crystal plasticity the deformation gradient is assumed to be multiplicatively decomposed in its elastic and plastic parts as (see e.g., Asaro (1983)): such that and are the elastic and plastic deformation gradients, respectively. The elastic and plastic deformation gradients define two deformed configurations: one intermediate configuration described by , and a final deformed configuration . Here, the change in the crystal shape due to dislocation motion is accounted for in the plastic deformation gradient tensor, , the elastic deformation gradient tensor, , accounts for recoverable elastic stretch and rotations of the crystal lattice,

For a thermo-mechanical problem, a third configuration is introduced accounting for thermal deformations (see e.g., Li et al. (2019), Ozturk et al. (2016), and Meissonnier et al. (2001)). The resulting decomposition reads (1) where is the thermal deformation gradient, such that . The thermal deformation gradient accounts for the deformation of the crystal lattice due to thermal expansion. The constitutive equation and calculation details associated with the thermal deformation gradient are included in ComputeCrystalPlasticityThermalEigenstrain.

The total plastic velocity gradient can be expressed in terms of the plasticity deformation gradient as (2) This formulation is used to compute the updated plastic deformation gradient via backward time integration, i.e., (3) where is the second order identity tensor, the subscript denotes the current step, denotes the previous step, and is the time step size. The plastic deformation gradient is used to calculate the elastic deformation gradient via Eq. (1), which is then used in the computation of the elastic Lagrangian strain. The elastic Lagrangian strain is defined as (4) Let be the second Piola-Kirchhoff tensor, the stress that is work conjugate to . An elastic constitutive relation is given by (5) where is the fourth-order temperature dependent elasticity tensor. The stress is the pull back of the Cauchy stress () from the current configuration which is, (6)

To account for multiple deformation mechanisms, the total plastic velocity gradient () is computed as the sum of plastic velocity gradients coming from each crystal plasticity constitutive equations, (7) where is the plastic velocity gradient corresponding to th th crystal plasticity deformation mechanism, is the total number of deformation modes. Here, is defined as the sum of the slip increments on all of the slip systems (Asaro, 1983), (8) where is the slip rate for the the model on the slip system . Note that the associated slip direction and slip plane normal unit vectors, and , are defined in the reference configuration. The evolution of the plastic slip must be specified for every slip plane and every slip mechanism, which can be expressed as (9) which can take different forms among constitutive models used in crystal plasticity. Here, the denotes the slip resistance and denotes the resolved shear stress that is associated with slip system and model , respectively.

The resolved shear stress is defined as (10) Here, we report the shear stress in a form that considers the thermal effect. For readers who are particularly interested in the thermal eigenstrain calculations, please refer to the ComputeCrystalPlasticityThermalEigenstrain documentation page.

To facilitate the understanding of the above constitutive equations, some fundamental continuum mechanics concepts are included in the following subsections.

Calculation of Schmid Tensor

The calculation of the flow direction Schmid tensor, the dyadic product of the slip direction and slip plane normal unit vectors, , is straight forward for the case of cubic crystals, including Face Centered Cubic (FCC) and Body Centered Cubic (BCC) crystals. The 3-index Miller indices commonly used to describe the slip direction and slip plane normals are first normalized individually normalized and then directly used in the dyadic product.

Conversion of Miller-Bravais Indices for HCP to Cartesian System

Hexagonal Close Packed (HCP) crystals are often described with the 4-index Miller-Bravais system: (17) To compute the Schmid tensor from these slip direction and slip plane normals, the indices must first be transformed to the Cartesian coordinate system. Within the associated ComputeMultipleCrystalPlasticityStress implementation, this conversion uses the assumption that the a-axis, or the H index, align with the x-axis in the basal plane of the HCP crystal lattice, see Figure 1. The c-axis, the L index, is assumed to be paralled to the z-axis of the Cartesian system.

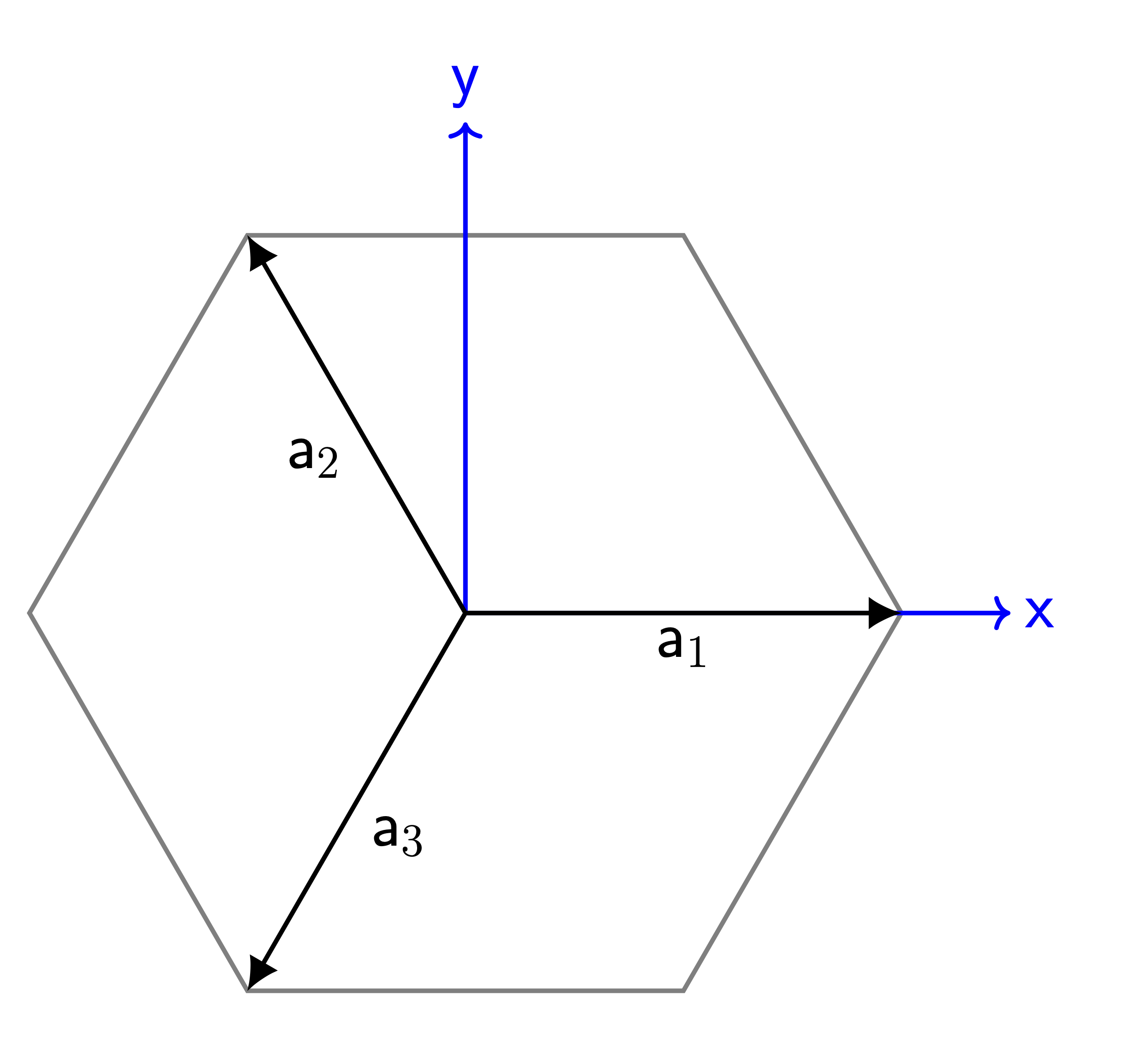
Figure 1: The convention used to transform the 4-index Miller-Bravais indices to the 3-index Cartesian system aligns the x-axis with the a-axis in the basal plane in this implementation.

The slip plane directions are transformed to the Cartesian system with the matrix equation (18)

where a and c are the HCP unit cell lattice parameters in the basal and axial directions, respectively. A check is performed with the basal plane indices to ensure that those indices sum to zero (). If the slip direction indices are given as decimal values, nummerical round-off errors may require an increase in the value of the parameter zero_tol which is used within the code to set the allowable deviation from exact zero.

The slip plane normals are similiarly transformed as (19)

Once transformed to the Cartesian system, these vectors are normalized and then used to compute the Schmid tensor.

commentnote

The alignment of the a axis of the Miller-Bravais notation and the x-axis of the Cartesian system within the basal plane of the unit HCP is specifically adopted for the conversion implementation in the ComputeMultipleCrystalPlasticityStress associated classes. While there is broad consensus in the alignment of the HPC c-axis with the Cartesian z-axis, no standard for alignment within the basal plane is clear. Users should note this assumption in the construction of their simulations and the interpretations of the simulation results.

Calculation of Crystal Rotation

The rotation of a crystal during deformation is calculated within the ComputeMultipleCrystalPlasticityStress class through a polar decomposition on the elastic part of the deformation tensor (), i.e.,

where is the symmetric matrix that describes the elastic stretch of the crystal, is the orthogonal tensor that describes the elastic part of the crystal rotation.

Note here represents the rotation of the crystal with respect to its crystal lattice. To obtain the the crystal rotation relative to the reference frame (total rotation ), initial orientation of the crystal needs to be considered, i.e.,

where denotes the rotation matrix that corresponds to the initial orientation of the crystal.

To obtain the Euler angles for the crystals during deformation, one will need to transform the rotation matrix to the Euler angle. One can refer to the ComputeUpdatedEulerAngle class for this purpose.

Computation Workflow

The order of calculations performed within the ComputeMultipleCrystalPlasticityStress class is given in flowchart form, Figure 2. The converged Cauchy stress value and the corresponding strain measure are then calculated, via the inverse of Eq. (16), before continuing the FEM residual calculation within the MOOSE framework.

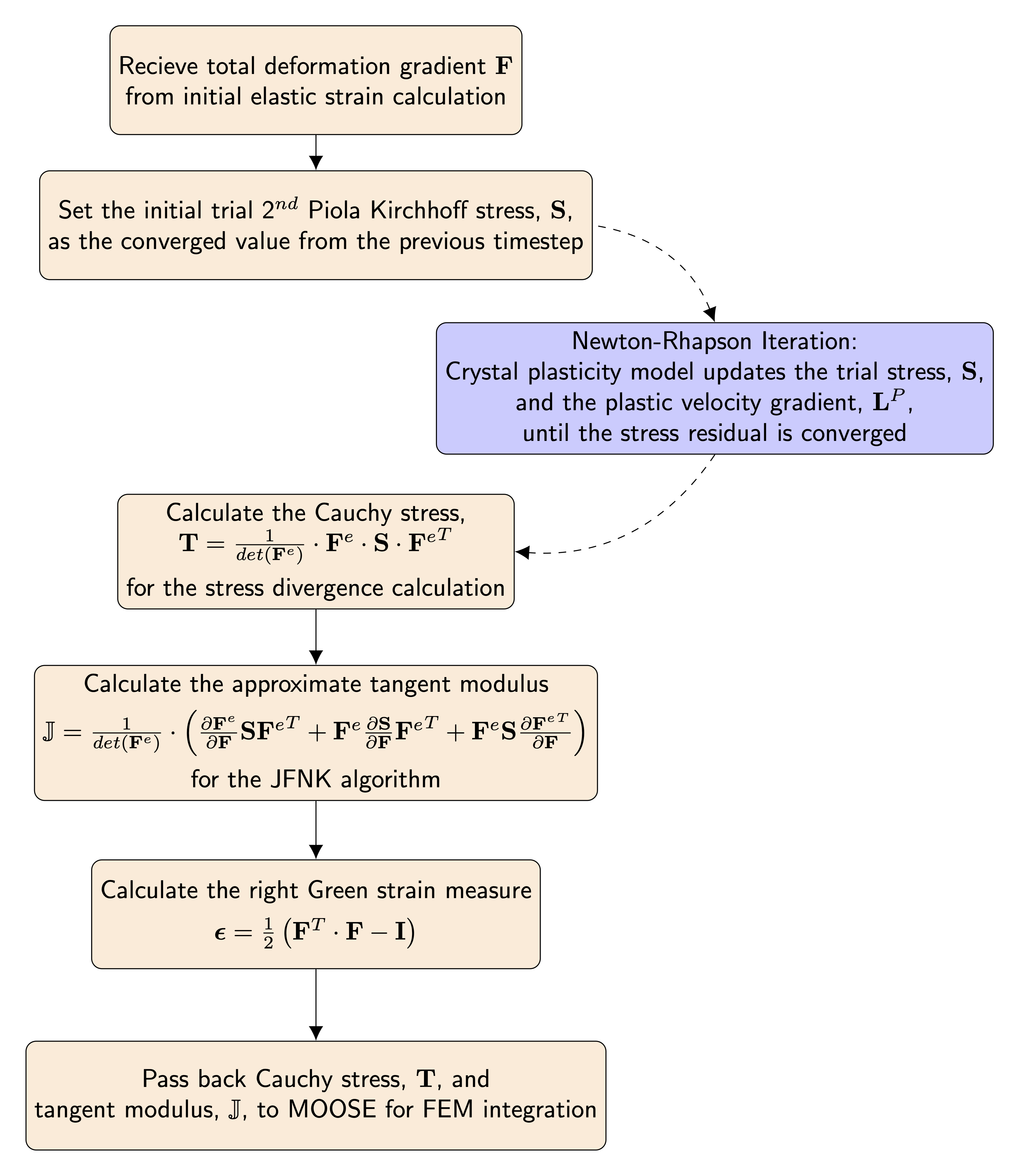
Figure 2: The flowchart for the calculation of the stress and strain measures within the ComputeMultipleCrystalPlasticityStress class as implemented in the tensor mechanics module of MOOSE is shown here. The components involved in the Newton-Rhapson iteration are shown in light blue and the components shown in light orange are executed once per MOOSE iteration.

Using a Newton Rhapson approach, outlined below in Figure 3, we consider the system converged when the residual of the second Piola-Kirchhoff stress increments from the current and previous iterations is within tolerances specified by the user.

The Newton-Rhapson iteration algorithm implemented in CrystalPlasticityStressUpdateBase separates the iteration over the second Piola-Kirchhoff stress residual from the physically based constitutive models used to calculate the plastic velocity gradient, see Figure 3. The convergence algorithm for Newton-Rhapson iteration is taken from other approaches already implemented in MOOSE and is adapted for our crystal plasticity framework.

Figure 3: The algorithm components of the Newton-Rhapson iteration are shown in light blue and the crystal plasticity constitutive model components, which should be overwritten by a specific constitutive model class inheriting from CrystalPlasticityStressUpdateBase, are shown in light green.

Constitutive models are used to calculate the plastic slip rate in classes which inherit from CrystalPlasticityStressUpdateBase.

Units Assumed in the Crystal Plasticity Materials

The simulation domain for crystal plasticity models is resolved on the order of individual crystal grains, and, as such, the mesh size is small. Although MOOSE itself is dimension agnostic, the crystal plasticity models are implemented in the mm-MPa-s unit system. This dimension system choice impacts the input files in the following manner:

• Mesh dimensions should be constructed in mm

• Elastic constant values (e.g. Young's modulus and shear modulus) are entered in MPa

• Initial slip system strength values are entered in MPa

• Simulation times are given in s

• Strain rates and displacement loading rates are given in 1/s and mm/s, respectively

In physically based models, which maybe based on this class, initial densities of crystal defects (e.g. dislocations, point defects) should be given in 1/mm or 1/mm

Example Input File

[./stress]
  type = ComputeMultipleCrystalPlasticityStress
  crystal_plasticity_models = 'trial_xtalpl'
  tan_mod_type = exact
[../]

Note that the specific constitutive crystal plasticity model must also be given in the input file to define the plastic slip rate increment

[./trial_xtalpl]
  type = CrystalPlasticityKalidindiUpdate
  number_slip_systems = 12
  slip_sys_file_name = input_slip_sys.txt
[../]

Finally a specific constant elasticity tensor class must be used with these materials to account for the use of the slip planes and directions in the reference configuration, Eq. (7), Eq. (8), and Eq. (10),

[./elasticity_tensor]
  type = ComputeElasticityTensorCP
  C_ijkl = '1.684e5 1.214e5 1.214e5 1.684e5 1.214e5 1.684e5 0.754e5 0.754e5 0.754e5'
  fill_method = symmetric9
[../]

Input Parameters

References