1D Reflection Benchmark
This document describes the 1D metal-backed dielectric slab benchmark / verification test for the electromagnetics module. This is based on Section 3.4 in (Jin, 2014). The goal of the benchmark is to accurately determine the power reflected by the slab when impinged by an electric plane wave, compared to an analytic solution. Below is a summary of the test, along with relevant background theory, results, and the test input file for review.
Model Geometry
The geometry used in this benchmark is shown below in Figure 1.
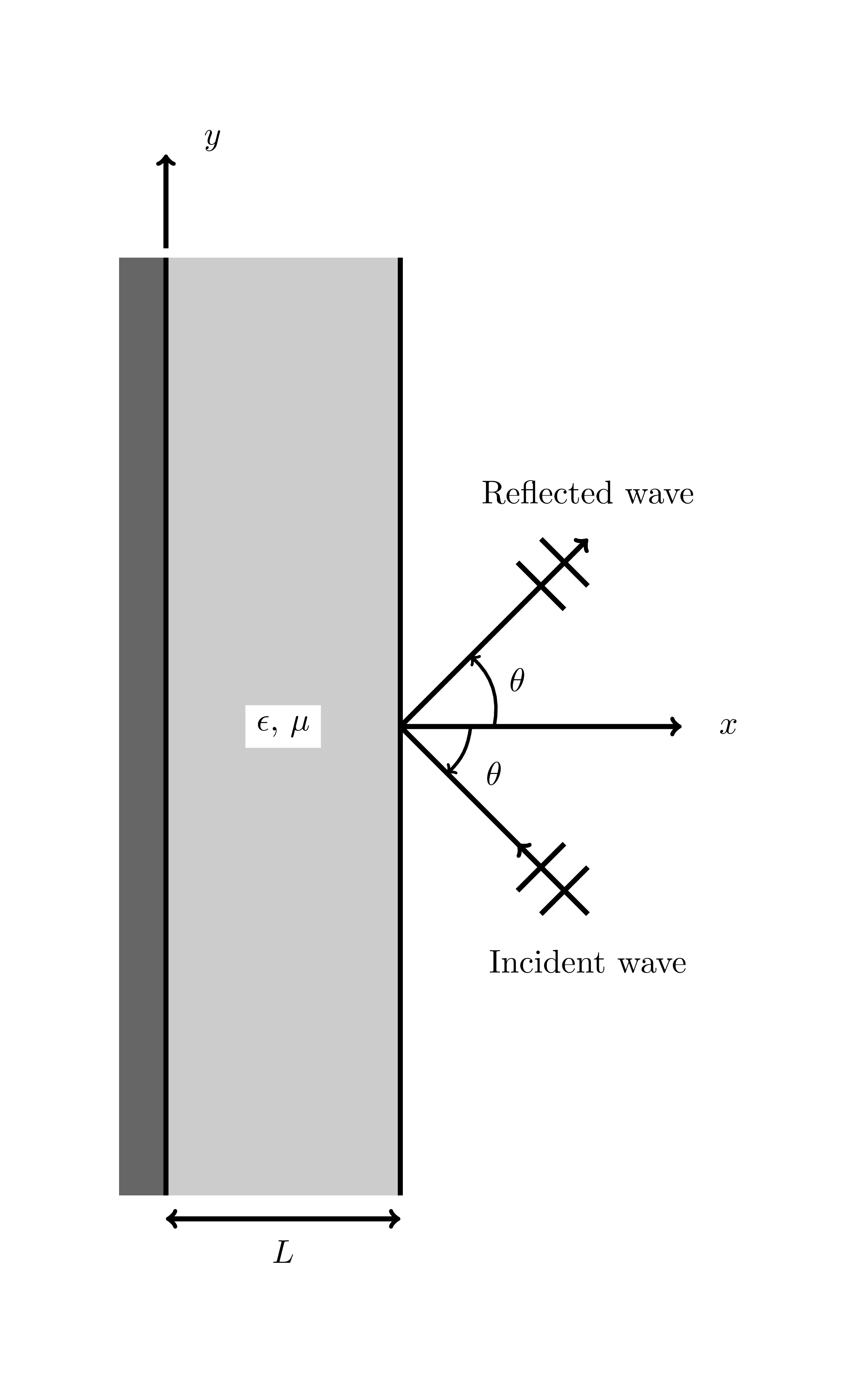
Figure 1: Slab reflection benchmark geometry.
Governing Equations and Boundary Condition
As described in (Jin, 2014), this benchmark models a uniform plane wave striking an inhomogeneous dielectric backed by a perfectly conducting grounded plane. The slab, shown in Figure 1, has a thickness , a relative permittivity , and a relative permeability . Both material properties are functions of position in the slab. The medium outside the slab is free space (). An -polarized plane wave is the incoming wave, and can be represented in general by
where
is the magnitude of the incident field,
is the wavenumber () where is the wavelength),
, and
is the incidence angle of the wave.
The general scalar Helmholtz equation governing the electric field in this scenario is given by
(1)The boundary condition on the conducting backing plane is given by
(2)which is implemented in code by DirichletBC and the boundary condition just inside the slab interface with free space is given by
which is implemented in code by EMRobinBC.
Model Parameters and Functions
The JinSlabCoeffFunc test function object (located in modules/electromagnetics/test/src/functions) is used in this benchmark to represent the coefficient shown in Eq. (1). The complex-valued function is
The relative electric permittivity in the model is defined as
and the relative magnetic permeability is defined as
Other model parameters are shown below in Table 1.
Table 1: Constant model parameters for the slab reflection benchmark study.
| Parameter (unit) | Value |
|---|---|
| Wave frequency (MHz) | 20 |
| Wavelength, (m) | 15 |
| Wavenumber, (1/m) | / |
| Slab thickness, (m) | 75 |
| Incident wave magnitude, (V/m) | 1 |
Analytic Solution for Reflection Coefficient
The analytic solution approach is outlined in (Jin, 2014), Section 3.4.2, but will be summarized here. First the slab in Figure 1 should be divided into thin layers as shown in Figure 2, and the analytic solution to the original Helmholtz equation in Eq. (1) in a single layer should be found.
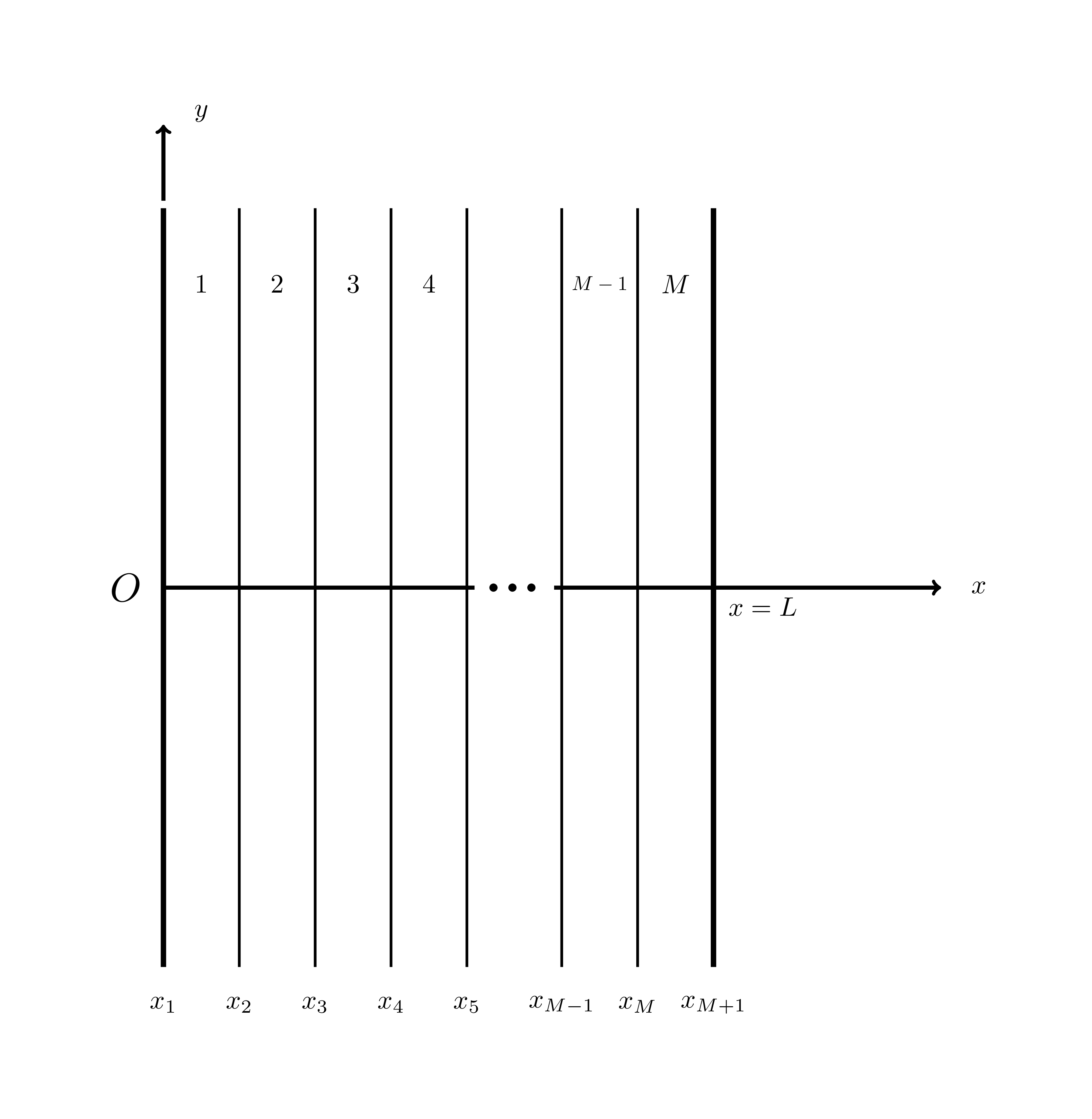
Figure 2: Slab reflection benchmark geometry, cut into layers.
This solution can be shown to be
where and are unknown constant coefficients. Enforcing continuity across the layer interfaces in the direction, we can find the wave reflection coefficient for the interface between the th and th layer to be
where
Given the DirichletBC placed on the metal surface in Eq. (2), it can be found that . Thus, the analytic solution can be determined recursively for the desired number of layers. The coefficient reported below in Figure 3 represents the magnitude of the coefficient , over a range of frequencies on the dielectric interface.
ReflectionCoefficient object
The postprocessor object used in this benchmark to calculate the percentage of reflected power is described in more detail in the ReflectionCoefficient documentation. To summarize, the object evaluates the following expression:
which assumes -polarized plane waves as used in this benchmark. Because wave power is proportional to the magnitude of the wave squared, the coefficient reported below in the results section representing the percentage of reflected power is
Input File
# 1D metal backed dielectric slab benchmark (electric field edition)
# Based on Section 3.4 of Jin, "The Finite Element Method in Electromagnetics, 3rd Ed."
# frequency = 20 MHz
# eps_R = 4 + (2 - j0.1)(1 - x/L)^2
# mu_R = 2 - j0.1
# L = 5 * wavelength
k = 0.41887902047863906 # 2 * pi * 20e6 / 3e8
L = 75 # = 5 * c / freq. (in m)
E0 = 1 # magnitude of the incident field (in V/m)
theta = 0 # wave incidence angle, in degrees
[GlobalParams]
theta = ${theta}
[]
[Mesh]
[slab]
type = GeneratedMeshGenerator
dim = 1
nx = 100
xmin = 0
xmax = ${L}
[]
[rename]
type = RenameBoundaryGenerator
input = slab
old_boundary = 'left right'
new_boundary = 'metal vacuum'
[]
[]
[Variables]
[E_real]
order = FIRST
family = LAGRANGE
[]
[E_imag]
order = FIRST
family = LAGRANGE
[]
[]
[Functions]
[coeff_real]
type = JinSlabCoeffFunc
k = ${k}
length = ${L}
component = real
[]
[coeff_imag]
type = JinSlabCoeffFunc
k = ${k}
length = ${L}
component = imaginary
[]
[negative_coeff_imag]
type = JinSlabCoeffFunc
k = ${k}
length = ${L}
coef = -1
component = imaginary
[]
[cosTheta]
type = ParsedFunction
expression = 'cos(${theta})'
[]
[]
[Materials]
[coeff_real_material]
type = ADGenericFunctionMaterial
prop_names = coeff_real_material
prop_values = coeff_real
[]
[coeff_imag_material]
type = ADGenericFunctionMaterial
prop_names = coeff_imag_material
prop_values = coeff_imag
[]
[negative_coeff_imag_material]
type = ADGenericFunctionMaterial
prop_names = negative_coeff_imag_material
prop_values = negative_coeff_imag
[]
[]
[Kernels]
[diffusion_real]
type = Diffusion
variable = E_real
[]
[field_real]
type = ADMatReaction
reaction_rate = coeff_real_material
variable = E_real
[]
[coupled_real]
type = ADMatCoupledForce
mat_prop_coef = negative_coeff_imag_material
v = E_imag
variable = E_real
[]
[diffusion_imag]
type = Diffusion
variable = E_imag
[]
[field_imag]
type = ADMatReaction
reaction_rate = coeff_real_material
variable = E_imag
[]
[coupled_imag]
type = ADMatCoupledForce
mat_prop_coef = coeff_imag_material
v = E_real
variable = E_imag
[]
[]
[BCs]
[metal_real]
type = DirichletBC
value = 0
variable = E_real
boundary = metal
[]
[metal_imag]
type = DirichletBC
value = 0
variable = E_imag
boundary = metal
[]
[vacuum_real]
type = EMRobinBC
coeff_real = ${k}
func_real = cosTheta
profile_func_real = ${E0}
boundary = vacuum
component = real
field_real = E_real
field_imaginary = E_imag
variable = E_real
sign = negative
[]
[vacuum_imag]
type = EMRobinBC
coeff_real = ${k}
func_real = cosTheta
profile_func_real = ${E0}
boundary = vacuum
component = imaginary
field_real = E_real
field_imaginary = E_imag
variable = E_imag
sign = negative
[]
[]
[Postprocessors]
[reflection_coefficient]
type = ReflectionCoefficient
k = ${k}
length = ${L}
incoming_field_magnitude = ${E0}
field_real = E_real
field_imag = E_imag
boundary = vacuum
outputs = 'csv console'
[]
[]
[Preconditioning]
[smp]
type = SMP
full = true
[]
[]
[Executioner]
type = Steady
solve_type = NEWTON
petsc_options_iname = '-pc_type'
petsc_options_value = 'lu'
[]
[Outputs]
exodus = false
csv = true
print_linear_residuals = true
[]
Results and Discussion
The input file shown above was swept over a range of angles from to , and the results for 100 elements compared to the analytic solution are shown below in Figure 3, where there is good agreement with the analytical solution. Jin also saw a deviation between the analytic solution and the finite element solution corresponding to smaller angles of incidence. They attributed this deviation to the idea that as increases, the magnitude of the coefficient in the second term of Eq. (1) decreases. In physical terms, this means that there will be slower field variation in the -direction as we approach , giving more consistent results between the two solutions. A 1D model might not be adequate to capture the reflection exactly with smaller .
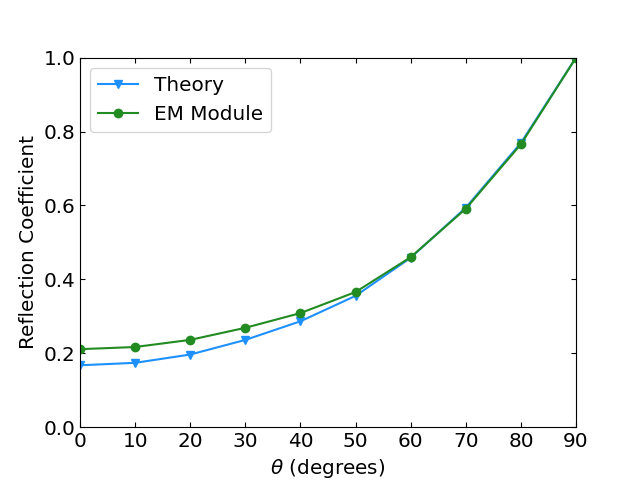
Figure 3: Slab reflection benchmark results.
References
- Jian-Ming Jin.
The Finite Element Method in Electromagnetics.
John Wiley & Sons, Hoboken, New Jersey, USA, 3rd edition, 2014.[BibTeX]